In the rapidly evolving world of AI within materials and chemicals industries, Bayesian optimization (BO) has re-emerged as a powerful tool. Its ability to efficiently use small amounts of data to improve decision-making has made it a popular choice among researchers. However, despite its impressive capabilities and recent advancements, BO is not a one-size-fits-all solution, especially when it comes to the specific needs of commercial materials and chemicals companies. In this blog post, we will explore why BO may not be suitable for all AI purposes in this domain.
Recent Progress in Bayesian Optimization
Bayesian optimization is a long-standing technique that has seen progress in recent years. Its core strength lies in its ability to make intelligent trade-offs between exploration and exploitation, allowing researchers to efficiently search for optimal solutions in complex landscapes. Using a BO framework with models such as Gaussian Process Regression (GPR) and acquisition functions like Expected Improvement (EI) have demonstrated great utility.
Limitations of Bayesian Optimization in Industrial Applications
Speed
Despite its strengths, Bayesian optimization encounters several challenges when applied to the reformulation of materials and chemicals in the real world. One of the primary concerns is the time constraint. Companies in this sector operate under tight schedules, requiring AI models to generate actionable results within an hour or less. This rapid turnaround is crucial for enabling researchers to iterate on their ideas and promptly move into laboratory experimentation. Unfortunately, traditional BO is computationally intensive, with time to run scaling exponentially with the number of dimensions under consideration. What works well for optimizing reactor conditions would be impossibly slow when considering all the ingredients on your shelf.

The Complexity of Materials and Chemicals Search Spaces
Another significant limitation arises from the inherent complexity of the search spaces involved in materials and chemicals work. Unlike many traditional optimization problems, these search spaces are both high-dimensional and discontinuous. For instance, a typical formulation might involve selecting from 30 to 50 raw materials, each of which can contribute anywhere from 0 to 100% of the total mixture and many of which may be incompatible. Additionally, there are multiple processing steps, each with several setting options, and the sequence of these steps can drastically impact the outcome. This results in a search space that is not only vast but also characterized by abrupt changes and non-linear interactions.
Bayesian optimization, while adept at handling certain types of complex spaces, can struggle in such environments. The high dimensionality and discontinuities make it difficult to model the landscape accurately, and the potential for numerous local optima can lead to suboptimal solutions.
Complexity of Multi-Objective and Constraint Handling
Real-world materials design almost always involves multiple objectives and various constraints. A new material might need to maximize performance (strength, efficiency, etc.) while minimizing cost or toxicity, and satisfying constraints on stability or manufacturability. Handling this within a Bayesian optimization framework is not easy. Standard BO is inherently single-objective, seeking the maximum of one reward function. Researchers have extended Bayesian optimization to multi-objective scenarios (termed MOBO or multi-objective Bayesian optimization) by modeling a vector of objectives and searching for Pareto-optimal solutions.
While these methods exist, they substantially increase complexity: multiple Gaussian Processes (one per objective) or a multi-output GP with a cross-covariance must be maintained, and acquisitions require integrating trade-offs. Moreover, Bayesian optimization doesn’t inherently provide a way to enforce hard constraints, except by augmenting the model or acquisition function (e.g., modeling constraint satisfaction probability and multiplying it into the acquisition function).
Interpretability
One of the most exciting parts of using AI in research is when an underlying connection between your inputs and outputs suddenly becomes clear. For a scientist or engineer, understanding why a certain candidate is suggested or which variables are driving the model’s decisions can be as valuable as the suggestion itself. Traditional Bayesian Optimization treats the problem as a black-box optimization. While GPR does have hyperparameters (lengthscales) that indicate which features are more influential, and one can visualize partial dependence, these insights are fairly abstract and difficult for chemical researchers to interpret. This problem is exacerbated if you use variable reduction to make computations run in reasonable time, moving the complexity out of the optimization and into the interpretation.
So what’s the alternative?
Random Forests with Uncertainty Estimates for Learning Sequentially
Citrine’s sequential learning approach represents a new generation of optimization frameworks that build on Bayesian Optimization’s foundations while overcoming many of its limitations. By swapping the GPR for a more scalable and robust model (random forests with advanced uncertainty quantification), Citrine’s platform retains the data-efficiency and intelligence of BO but gains the ability to handle bigger, real-word problems (dozens of variables, multiple objectives, noisy data, and real-world constraints) with ease. It provides results that are not only optimal but explainable – a critical factor for trust in AI-driven design in the research community.
Interpretability
Random forests provide many avenues for interpretability. Random forests naturally ignore inputs in the parts of your operating regime where they don’t contribute, meaning there’s no need for variable reduction. Citrine’s implementation offers built-in tools to compute feature importances (measuring how much each input contributes to reducing prediction error) and even Shapley values for each prediction to quantify the contribution of each feature to a particular candidate’s predicted performance (GitHub – CitrineInformatics/lolo: A random forest). This means when the model suggests, say, a new chemical formulation, the scientist can be shown which ingredients or processing parameters most increased the predicted target value. Such explanations build trust in the model and can yield scientific discoveries (for example, revealing that a certain element in an alloy is consistently associated with high performance might suggest a new design rule). The Citrine platform thus serves not just as an optimizer, but also as a collaborator that can point researchers to important structure–property relationships, making the optimization process more informed.
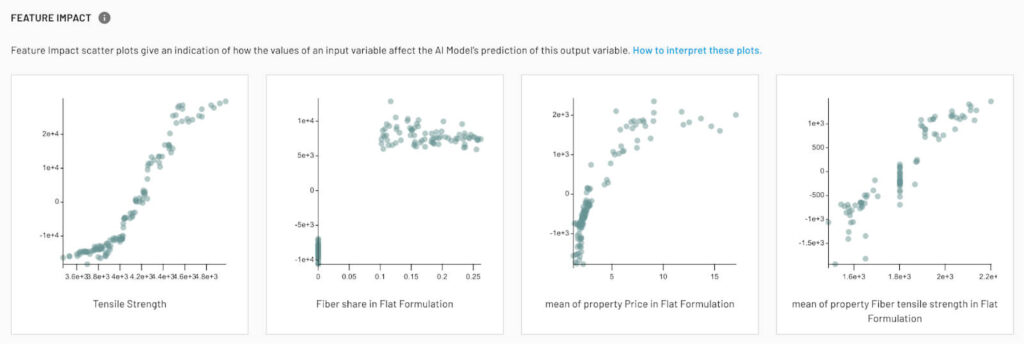
Practical Suggestions
It also reduces the risk of unphysical or impractical suggestions: by building in chemical rules and leveraging past data, the algorithm avoids “naïve” suggestions that a human would have ruled out immediately. For example, a GP-based BO might mathematically propose an exotic composition that is chemically unstable because it only sees a black-box function; Citrine’s model, adapted by researchers to include domain rules, and using a sophisticated discontinuous search space constrained using the researcher’s experience, would not waste time on that. In sum, the Citrine platform aligns the optimization process with scientific intuition and knowledge, whereas classical BO, while powerful, remains more of a black-box method requiring careful oversight to ensure it stays on realistic paths.
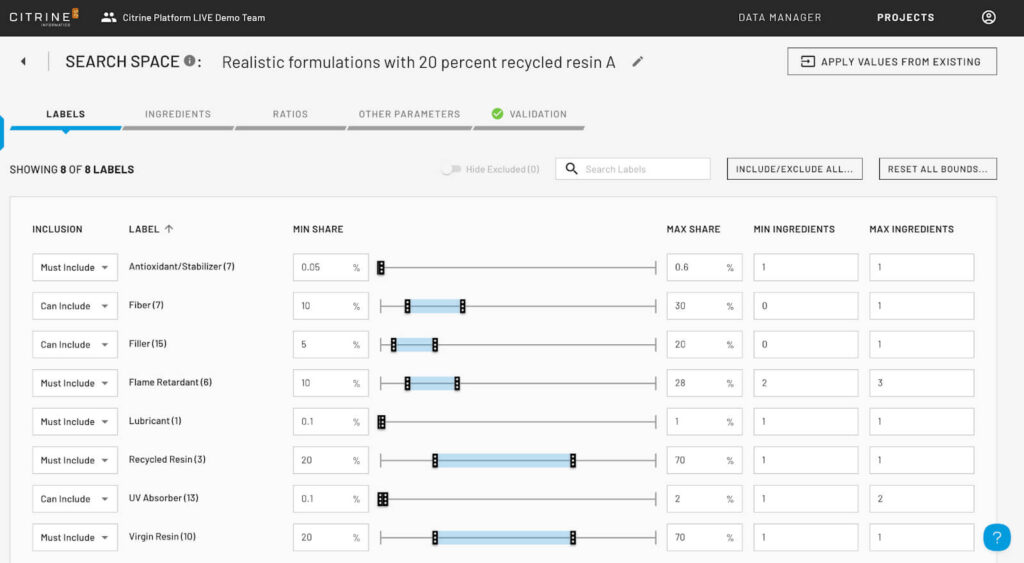
Speed
Importantly, this approach does not sacrifice performance: it matches the effectiveness of state-of-the-art BO in finding optimal materials, while delivering speed and flexibility improvements. As well as swapping GPR for Random Forests, the Citrine approach uses a modified Markov Chain Monte Carlo approach to traverse the search space efficiently, allowing us to guarantee results in a given time, rather than having to wait for an all-or-nothing slow computation.
Other Options
While Citrine’s default model that is automatically generated from the data is based on Random Forests, that doesn’t stop other approaches being used in the Citrine Platform. Linear Ensemble, Gaussian Process and Support Vector Machine can also be used. The platform can run all of the options and provide results from the model with the highest accuracy. If you have a favorite model in scikit-learn, you can add it to your optimization.
Conclusion
Bayesian optimization has had a profound impact on materials and chemical research, proving that machine learning can guide experiments to breakthroughs with far fewer trials than traditional methods. Its strengths—data efficiency, principled use of uncertainty, and strong theoretical foundation—made it an appealing choice for early demonstrations of autonomous materials discovery (Benchmarking the performance of Bayesian optimization across multiple experimental materials science domains | npj Computational Materials). However, bayesian methods based on Gaussian processes encounter scalability issues in high-dimensional or combinatorial design spaces (Race to the bottom: Bayesian optimisation for chemical problems – Digital Discovery (RSC Publishing) DOI:10.1039/D3DD00234A). They often assume a single-objective, noise-controllable scenario, whereas real projects involve multiple goals, complex constraints, and messy data. They function as black boxes at a time when interpretability and integration of domain expertise are increasingly required for adoption in practical R&D.
Bayesian optimization remains a valuable baseline and is still well-suited for certain academic and low-dimensional problems. Its legacy in introducing active learning to materials science is unquestionable. But for modern industrial chemicals design, which demands handling high complexity, incorporating expert knowledge, and providing actionable insights, something different is needed. Citrine Informatics’ approach exemplifies how the field is moving towards more holistic and robust sequential learning frameworks. These newer methods embrace uncertainty without being handcuffed by strict Bayesian formalisms, leverage ensemble models for scalability, and integrate domain knowledge for credibility. The result is an optimization platform that can accelerate innovation not just in theory, but in practice – guiding scientists to better materials, faster, and with greater confidence in the outcomes.