Machine learning (ML) has become a central tool for enabling researchers to discover and design new materials and chemicals. But gathering high-quality data for training ML models is expensive. In fact, collecting a new data point often requires carefully-planned laboratory experiments which utilize specialized equipment operated by trained experts. To gather data in a cost-effective manner, researchers and engineers are tuning to something called sequential learning (SL), or active learning, in which ML is used to predict the optimal data point to measure next. The measured data is then added to existing models in an iterative manner with the goal of reducing the number of experiments needed to realize a specific material performance metric.
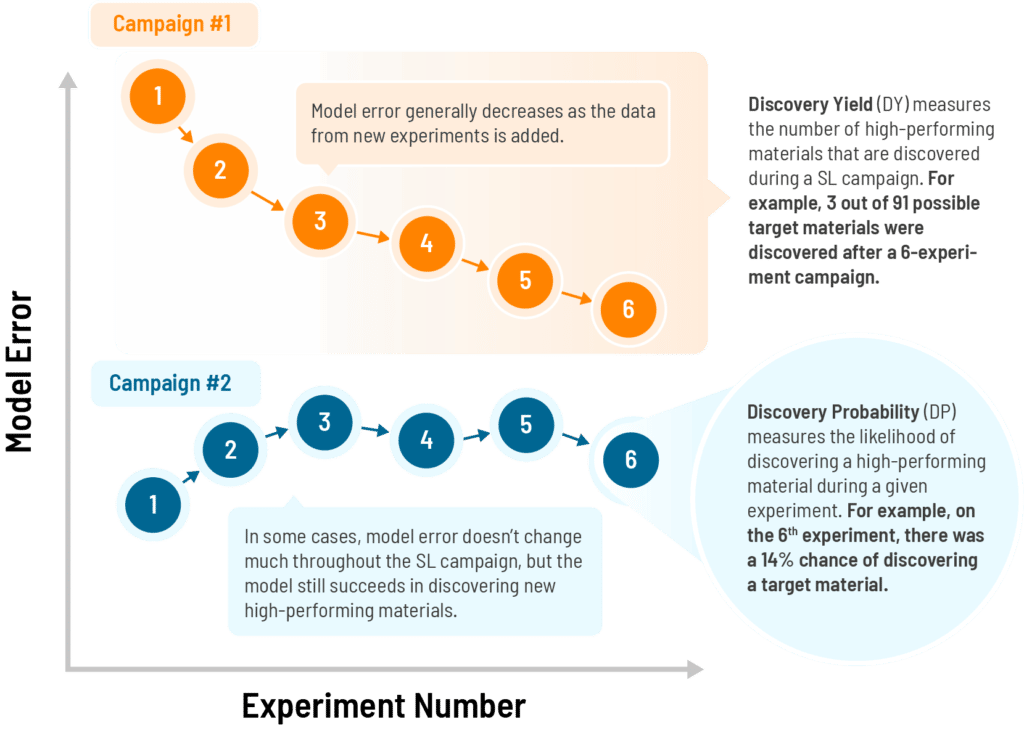
During the SL process, the performance of an ML model is often quantified using simple statistical measures such as root-mean-square error (RMSE). At first glance, one would assume that models with low RMSE should be most effective at guiding materials discovery via SL. To quantify this intuition, Citrine and collaborators at Stanford and Argonne National Lab studied how many experiments were required before different SL workflows were able to identify the optimal material candidates inside a specific search space. Surprisingly, we found that model error metrics such as RMSE were not good indicators of whether a given model could be used to successfully identify target materials.
Instead, we found that project success is largely driven by subtleties which are specific to each unique materials discovery problem. These include the distribution of target properties inside the search space, the number of unique target materials that the researcher hopes to find, whether uncertainty is considered when selecting experiments, and the total number of experiments performed throughout the SL process. In some cases, models that discover a target material quickly may have limited success in discovering the second and third target materials. Models which perform poorly when scored by traditional error metrics can still be successful in discovering optimal materials in the search space. And high-scoring models models may be successful at discovering materials in one range of target values, but unsuccessful in another. In light of these results, we designed novel metrics for predicting whether SL will achieve success for a given design goal. These include Discovery Yield (DY), a measure of how many high-performing materials are discovered during a simulated SL campaign, and Discovery Probability (DP), a measure of the likelihood of discovering high-performing materials during any given experiment in the SL process.
Our findings illustrate the importance of designing a modeling and discovery workflow which is highly tailored toward the specific problem of interest. In ML and SL for materials discovery, one size does not fit all, traditional error metrics may not be a good predictor of success, and the specifics of the design challenge have important implications for the optimal configuration of materials discovery strategies.
The pre-print for this publication can be found on arxiv: https://arxiv.org/abs/2210.13587.